Law of Conservation of Energy

The Law of Conservation of Energy states that in a close, isolated system, energy is not created or destroyed, but rather, is conserved. Kinetic and Potential Energy are used for Conservation of Energy problems.

Formula of Conservation of Energy:

• E_i = E_f

• _{KEi + PEi = KEf + PEf} 

• ½ mv²_i  + mgh_i + ½ ks²_i = ½ mv²_f + mgh_f + ½ ks²_f

Units for Conservation of Energy:

• The SI unit is measured in joules (J).
• The American Unit is measured in calories.

Here is a video explaining the the Law of Conservation of Energy:

The video explains the Law of Conservation of Energy. It shows how to use the formula in a problem and see what you are looking for. It gives an example of conservation of energy. It gives multiple examples and how you find what you are looking for. It explains how you use kinetic and potential energy. It shows you how you could find the potential and kinetic energy. 

Example Problems:

1. A skier glides down a frictionless hill of 100 meters, the ascends another hill, of height 90 meters, as shown in the figure below. What is the speed of the skier when it reaches the top of the second hill?

The skier moves from point A to point B

The skier is in a conservative system, as the only force acting upon him is gravity. Instead of calculating the work done over the curved hills, we can construct an alternate path, because of the principle of path independence:

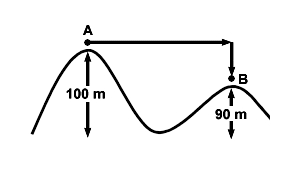
Theoretical Path of Skier

We construct a path of two segments: one is horizontal, going between the two hills, and one is vertical, accounting for the vertical drop between the two hills. What is the work done over each of these two segments? Since the gravitational force is perpendicular to the displacement in the horizontal segment, no work is done. For the second segment, the gravitational force is constant and parallel to the displacement. Thus the work done is: W = Fx = mgh = 10mg . By the Work-Energy Theorem, this net work causes an increase in velocity. If the skier started with no initial velocity, then we can relate the final velocity to the work done:

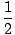 mv f 2 = 10mg

We can cancel the mass and solve for v f :

v f = 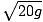 = 14m/s

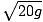Thus the final velocity of the skier is 14 m/s.

2. A block having mass 2kg and velocity 2m/s slide on the inclined plane. If the horizontal surface has friction constant µ=0, 4 find the distance it travels in horizontal before it stops.

We use conservation of energy in solution of this problem.

E_initial=E_final

E_initial=Ep+Ek=mgh+1/2mv² E_final=0

E_initial=2kg.10m/s².8m+1/2.2kg. (2m/s) ² Work done by friction=E_initial

E_initial=164 J

W_friction=µ.N.X=0,4.2kg.10m/s².X=E_i

8. X=164 J X=20,5m

Block slides 20,5m in horizontal

Screenshots of Roller Coaster:

The graph shows that the skater is at the beginning of the roller coaster. It has more potential energy because its at the top/its beginning.

The skater is at the bottom of the roller coaster. Whenever the skater is at the bottom its kinetic energy will be the greatest.








On this picture the skater is going around the loop. its kinetic energy is greater than potential energy because its on its way down the loop.